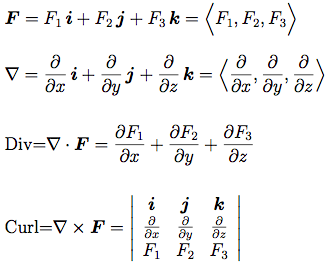Calculus 3: Divergence and Curl (25 of 50) Identity 1: DIV(F+G)=DIV(F)+DIV(G) - YouTube
DivCurl_000r.jpg
Untitled
Divergence - Wikipedia
Divergence and Curl calculator – GeoGebra
What is the divergence of vector F = xzi + yzj + xyk? - Quora
Solved Find the divergence of the vector field 3. divF - 6(1 | Chegg.com
Find the divergence of the vector field F at the given point | Quizlet
The Divergence of a Vector Field - YouTube
Answered: Find div F and curl F if F(x, Y, z) =… | bartleby
Answered: Find div F and curl F. F (x, y, z) =… | bartleby
Solved] Consider the vector field F = <xz, yz, xy > a. Calculate the... | Course Hero
Divergence of a Vector Field - Web Formulas
III.d Curl and Divergence Given a scalar function f(x, y, z) we have computed its gradient ∇f = ∂f ∂x i+ ∂f ∂y j+ ∂f
calculus - What if $\operatorname{div}f=0$? - Mathematics Stack Exchange
Consider the following vector field. F(x, y, z) = xyz i − x2y k (a) Find the curl of the vector - Brainly.com
Untitled
SOLVED: Consider the given vector field. F(x , Y, 2) = xyz i - x2y k (a) Find the curl of the vector field. curl F x+3xyj - xzk (b) Find the
![Calculus 3: Divergence and Curl (27 of 50) Identity 3: DIV(f G)=f [DIV(F)]+F [Gradient(f)] - YouTube](https://i.ytimg.com/vi/9oeAIN4n2Ko/hqdefault.jpg "Calculus 3: Divergence and Curl (27 of 50) Identity 3: DIV(f G)=f [DIV(F)]+F [Gradient(f)] - YouTube")
Calculus 3: Divergence and Curl (27 of 50) Identity 3: DIV(f G)=f [DIV(F)]+F [Gradient(f)] - YouTube
Ilectureonline
Solved] Calculate the divergence of the field 1 + x 2 + y 2 < x , y ,... | Course Hero
Divergence and Curl calculator – GeoGebra
Geneseo Math 223 03 Div and Curl
![Calculus 3: Divergence and Curl (31 of 50) Identity 7: CURL[CURL(F)]=Grad[ DIV(f)] – (Grad)^2(F) - YouTube](https://i.ytimg.com/vi/w1LxPgSRz94/hqdefault.jpg "Calculus 3: Divergence and Curl (31 of 50) Identity 7: CURL[CURL(F)]=Grad[ DIV(f)] – (Grad)^2(F) - YouTube")
Calculus 3: Divergence and Curl (31 of 50) Identity 7: CURL[CURL(F)]=Grad[ DIV(f)] – (Grad)^2(F) - YouTube
SOLVED:Plot the vector field and guess where div F > 0 and where div F < 0 . Then calculate div F to check your guess. F = ⟨x^2, y^2 ⟩
differential geometry - Motivation for constructing $F$ s.t. $\ker(\text{curl}) \subset \text{Im}(\text{grad})$, $\ker(\text{div}) \subset \text{Im}(\text{curl})$ - Mathematics Stack Exchange
Divergence - Wikipedia
